Z3约束初体验

0x01

• 拿一道CTF题目为例,主函数如下

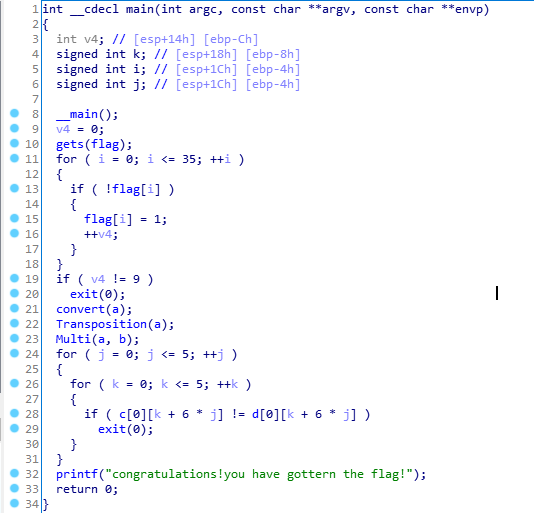
• 这是一个关于矩阵的题目。

• 思路很清晰,函数名称也直接表达出来函数作用了。 但是求解是现在的难题了。

• 如果考虑正向爆破… 难度太大太大,太费时间了, 毕竟有27个未知数呢。

• 为什么是27而不是36？ 因为根据

gets(flag);
for ( i = 0; i <= 35; ++i )
{
  if ( !flag[i] )
  {
    flag[i] = 1;
    ++v4;
  }
}
if ( v4 != 9 )
  exit(0);

• 需要让v4 = 9，那么也就需要 !flag[i]满足9次,而flag的大小是36, 即 只输入27个数就能满足题意。

• 现在需要提取出来题目给的矩阵(即题中的d)

d = [0x12027,0x0F296,0x0BF0E,0x0D84C,0x91D8,0x297,
    0x0F296,0x0D830,0x0A326,0x0B010,0x7627,0x230,
    0x0BF0E,0x0A326,0x8FEB,0x879D,0x70C3,0x1BD,
    0x0D84C,0x0B010,0x879D,0x0B00D,0x6E4F,0x1F7,
    0x91D8,0x7627,0x70C3,0x6E4F,0x9BDC,0x15C,
    0x297,0x230,0x1BD,0x1F7,0x15C,0x6]

• 网上找到一脚本:

#coding:utf-8
from z3 import *
#引入time模块只是为了看一看这个程序跑完需要多长时间
import time
t1 = time.time()
#创建一个解决方案实例
solver = Solver()
#flag长度先设置为36，包括尾部的9个1
flag = [Int('flag%d'%i) for i in range(36)]
#保存flag的矩阵
a = [i for i in flag]
#保存flag的转置矩阵
b = [i for i in range(36)]
#保存a*b的矩阵
c = [0 for i in range(36)]
#堆中正确flag的运算结果
d = [0x12027,0x0F296,0x0BF0E,0x0D84C,0x91D8,0x297,
    0x0F296,0x0D830,0x0A326,0x0B010,0x7627,0x230,
    0x0BF0E,0x0A326,0x8FEB,0x879D,0x70C3,0x1BD,
    0x0D84C,0x0B010,0x879D,0x0B00D,0x6E4F,0x1F7,
    0x91D8,0x7627,0x70C3,0x6E4F,0x9BDC,0x15C,
    0x297,0x230,0x1BD,0x1F7,0x15C,0x6]

#获得a的转置矩阵
for i in range(6):
    for j in range(6):
        b[i+6*j] = a[6*i+j]

#运算a*b
for i in range(6):
    for j in range(6):
        for k in range(6):
            c[j+6*i] = c[j+6*i] + a[6*i+k]*b[6*k+j]
        #添加约束，正确flag的运算结果
        solver.add(simplify(c[j+6*i]) == d[j+6*i])

#添加约束，除了尾部，flag的字符一定在可见字符范围内
for i in range(6,36-10):
    solver.add(flag[i]>=32)
    solver.add(flag[i]<=127)

#添加约束，由于flag有格式，前6位一定为whctf{
for i in range(6):
    solver.add(flag[i] == ord('whctf{'[i]))

#添加约束，根据题意flag的尾部为9个1
for i in range(36-9,36):
    solver.add(flag[i] == 0x1)

#添加约束，flag的最后一个肯定是}
solver.add(flag[-10] == ord('}'))

#这里一定要有，不check的话会报错
if solver.check() == sat:
    m = solver.model()
    f = ''
    #获得结果
    for i in range(36):
        f+=chr(eval(str(solver.model().eval(flag[i]))))
    #输出flag
    print f
else:
    print('error')
t2 = time.time()
print(t2-t1)

• 鉴于有27个未知数,正如求解27元方程组一般,如果知道的关系越多,那么求解起来越容易, 求解所用时间也就越少。

• 我把 “#添加约束，由于flag有格式，前6位一定为whctf{ “这个条件约束去掉以后再去跑的话 跑了74秒,而按照上面脚本跑的话,只需要3.2秒。

• 不难看出z3求解的约束条件就是把题中给的关系进行还原,然后让约束求解器进行求解,我们所须要做的工作就是把条件列出来。

---

• 顺带说一下 s.append(m[flag[i]].as_long()) 中的as_long()的大致作用。

• 如果去掉这个.as_long(),而只保留m[flag[i]]

• 则下面for i in s: 中的i的类型是instance类型,从而导致 flag+=chr(i)中的chr()方法无法正常使用(因为chr()里面需要传入int型的数据。)

• 所以这个as_long()的功能大概就是把数据转为int类型吧。

0x02

• 拿一道22元方程组求解的数学题目为例,直接上脚本了。

#coding:utf-8
from z3 import *
import time
t1 = time.time()

a = [Int('a%d'%i) for i in range(22)]

s = Solver()

s.add(2*a[0]+3*a[1]+5*a[2]+7*a[3]+11*a[4]+13*a[5]+17*a[6]+19*a[7]+23*a[8]+29*a[9]+31*a[10]+37*a[11]+41*a[12]+43*a[13]+47*a[14]+53*a[15]+59*a[16]+61*a[17]+67*a[18]+71*a[19]+73*a[20]+79*a[21]==83948)
s.add(83*a[0]+89*a[1]+97*a[2]+101*a[3]+103*a[4]+107*a[5]+109*a[6]+113*a[7]+127*a[8]+131*a[9]+137*a[10]+139*a[11]+149*a[12]+151*a[13]+157*a[14]+163*a[15]+167*a[16]+173*a[17]+179*a[18]+181*a[19]+191*a[20]+193*a[21]==321979)
s.add(197*a[0]+199*a[1]+211*a[2]+223*a[3]+227*a[4]+229*a[5]+233*a[6]+239*a[7]+241*a[8]+251*a[9]+257*a[10]+263*a[11]+269*a[12]+271*a[13]+277*a[14]+281*a[15]+283*a[16]+293*a[17]+307*a[18]+311*a[19]+313*a[20]+317*a[21]==602643)
s.add(331*a[0]+337*a[1]+347*a[2]+349*a[3]+353*a[4]+359*a[5]+367*a[6]+373*a[7]+379*a[8]+383*a[9]+389*a[10]+397*a[11]+401*a[12]+409*a[13]+419*a[14]+421*a[15]+431*a[16]+433*a[17]+439*a[18]+443*a[19]+449*a[20]+457*a[21]==917405)
s.add(461*a[0]+463*a[1]+467*a[2]+479*a[3]+487*a[4]+491*a[5]+499*a[6]+503*a[7]+509*a[8]+521*a[9]+523*a[10]+541*a[11]+547*a[12]+557*a[13]+563*a[14]+569*a[15]+571*a[16]+577*a[17]+587*a[18]+593*a[19]+599*a[20]+601*a[21]==1238849)
s.add(607*a[0]+613*a[1]+617*a[2]+619*a[3]+631*a[4]+641*a[5]+643*a[6]+647*a[7]+653*a[8]+659*a[9]+661*a[10]+673*a[11]+677*a[12]+683*a[13]+691*a[14]+701*a[15]+709*a[16]+719*a[17]+727*a[18]+733*a[19]+739*a[20]+743*a[21]==1565673)
s.add(751*a[0]+757*a[1]+761*a[2]+769*a[3]+773*a[4]+787*a[5]+797*a[6]+809*a[7]+811*a[8]+821*a[9]+823*a[10]+827*a[11]+829*a[12]+839*a[13]+853*a[14]+857*a[15]+859*a[16]+863*a[17]+877*a[18]+881*a[19]+883*a[20]+887*a[21]==1917643)
s.add(907*a[0]+911*a[1]+919*a[2]+929*a[3]+937*a[4]+941*a[5]+947*a[6]+953*a[7]+967*a[8]+971*a[9]+977*a[10]+983*a[11]+991*a[12]+997*a[13]+1009*a[14]+1013*a[15]+1019*a[16]+1021*a[17]+1031*a[18]+1033*a[19]+1039*a[20]+1049*a[21]==2280667)
s.add(1051*a[0]+1061*a[1]+1063*a[2]+1069*a[3]+1087*a[4]+1091*a[5]+1093*a[6]+1097*a[7]+1103*a[8]+1109*a[9]+1117*a[10]+1123*a[11]+1129*a[12]+1151*a[13]+1153*a[14]+1163*a[15]+1171*a[16]+1181*a[17]+1187*a[18]+1193*a[19]+1201*a[20]+1213*a[21]==2625651)
s.add(1217*a[0]+1223*a[1]+1229*a[2]+1231*a[3]+1237*a[4]+1249*a[5]+1259*a[6]+1277*a[7]+1279*a[8]+1283*a[9]+1289*a[10]+1291*a[11]+1297*a[12]+1301*a[13]+1303*a[14]+1307*a[15]+1319*a[16]+1321*a[17]+1327*a[18]+1361*a[19]+1367*a[20]+1373*a[21]==3001323)
s.add(1381*a[0]+1399*a[1]+1409*a[2]+1423*a[3]+1427*a[4]+1429*a[5]+1433*a[6]+1439*a[7]+1447*a[8]+1451*a[9]+1453*a[10]+1459*a[11]+1471*a[12]+1481*a[13]+1483*a[14]+1487*a[15]+1489*a[16]+1493*a[17]+1499*a[18]+1511*a[19]+1523*a[20]+1531*a[21]==3399957)
s.add(1543*a[0]+1549*a[1]+1553*a[2]+1559*a[3]+1567*a[4]+1571*a[5]+1579*a[6]+1583*a[7]+1597*a[8]+1601*a[9]+1607*a[10]+1609*a[11]+1613*a[12]+1619*a[13]+1621*a[14]+1627*a[15]+1637*a[16]+1657*a[17]+1663*a[18]+1667*a[19]+1669*a[20]+1693*a[21]==3746423)
s.add(1697*a[0]+1699*a[1]+1709*a[2]+1721*a[3]+1723*a[4]+1733*a[5]+1741*a[6]+1747*a[7]+1753*a[8]+1759*a[9]+1777*a[10]+1783*a[11]+1787*a[12]+1789*a[13]+1801*a[14]+1811*a[15]+1823*a[16]+1831*a[17]+1847*a[18]+1861*a[19]+1867*a[20]+1871*a[21]==4143323)
s.add(1873*a[0]+1877*a[1]+1879*a[2]+1889*a[3]+1901*a[4]+1907*a[5]+1913*a[6]+1931*a[7]+1933*a[8]+1949*a[9]+1951*a[10]+1973*a[11]+1979*a[12]+1987*a[13]+1993*a[14]+1997*a[15]+1999*a[16]+2003*a[17]+2011*a[18]+2017*a[19]+2027*a[20]+2029*a[21]==4553197)
s.add(2039*a[0]+2053*a[1]+2063*a[2]+2069*a[3]+2081*a[4]+2083*a[5]+2087*a[6]+2089*a[7]+2099*a[8]+2111*a[9]+2113*a[10]+2129*a[11]+2131*a[12]+2137*a[13]+2141*a[14]+2143*a[15]+2153*a[16]+2161*a[17]+2179*a[18]+2203*a[19]+2207*a[20]+2213*a[21]==4942889)
s.add(2221*a[0]+2237*a[1]+2239*a[2]+2243*a[3]+2251*a[4]+2267*a[5]+2269*a[6]+2273*a[7]+2281*a[8]+2287*a[9]+2293*a[10]+2297*a[11]+2309*a[12]+2311*a[13]+2333*a[14]+2339*a[15]+2341*a[16]+2347*a[17]+2351*a[18]+2357*a[19]+2371*a[20]+2377*a[21]==5356539)
s.add(2381*a[0]+2383*a[1]+2389*a[2]+2393*a[3]+2399*a[4]+2411*a[5]+2417*a[6]+2423*a[7]+2437*a[8]+2441*a[9]+2447*a[10]+2459*a[11]+2467*a[12]+2473*a[13]+2477*a[14]+2503*a[15]+2521*a[16]+2531*a[17]+2539*a[18]+2543*a[19]+2549*a[20]+2551*a[21]==5731505)
s.add(2557*a[0]+2579*a[1]+2591*a[2]+2593*a[3]+2609*a[4]+2617*a[5]+2621*a[6]+2633*a[7]+2647*a[8]+2657*a[9]+2659*a[10]+2663*a[11]+2671*a[12]+2677*a[13]+2683*a[14]+2687*a[15]+2689*a[16]+2693*a[17]+2699*a[18]+2707*a[19]+2711*a[20]+2713*a[21]==6177663)
s.add(2719*a[0]+2729*a[1]+2731*a[2]+2741*a[3]+2749*a[4]+2753*a[5]+2767*a[6]+2777*a[7]+2789*a[8]+2791*a[9]+2797*a[10]+2801*a[11]+2803*a[12]+2819*a[13]+2833*a[14]+2837*a[15]+2843*a[16]+2851*a[17]+2857*a[18]+2861*a[19]+2879*a[20]+2887*a[21]==6522731)
s.add(2897*a[0]+2903*a[1]+2909*a[2]+2917*a[3]+2927*a[4]+2939*a[5]+2953*a[6]+2957*a[7]+2963*a[8]+2969*a[9]+2971*a[10]+2999*a[11]+3001*a[12]+3011*a[13]+3019*a[14]+3023*a[15]+3037*a[16]+3041*a[17]+3049*a[18]+3061*a[19]+3067*a[20]+3079*a[21]==6954217)
s.add(3083*a[0]+3089*a[1]+3109*a[2]+3119*a[3]+3121*a[4]+3137*a[5]+3163*a[6]+3167*a[7]+3169*a[8]+3181*a[9]+3187*a[10]+3191*a[11]+3203*a[12]+3209*a[13]+3217*a[14]+3221*a[15]+3229*a[16]+3251*a[17]+3253*a[18]+3257*a[19]+3259*a[20]+3271*a[21]==7419507)
s.add(3299*a[0]+3301*a[1]+3307*a[2]+3313*a[3]+3319*a[4]+3323*a[5]+3329*a[6]+3331*a[7]+3343*a[8]+3347*a[9]+3359*a[10]+3361*a[11]+3371*a[12]+3373*a[13]+3389*a[14]+3391*a[15]+3407*a[16]+3413*a[17]+3433*a[18]+3449*a[19]+3457*a[20]+3461*a[21]==7843195)

print s.check()

if s.check() == sat:
    print s.model()
    m = s.model()
    L = []
    for i in range(22):
        L.append(m[a[i]])
    print L
t2 = time.time()
print(t2-t1),'s'

一些关于Z3的博文

传送门

传送门

传送门