
0x00 前言
0x01 Re
0x001 签到题
题目说是考察线性代数,但是可以通过Z3快速求解。
Z3脚本如下:
1 | # -*- coding: UTF-8 -*- |
0x02 DEBUG
- IDA动态调试即可拿到Flag。
0x02 Pwn
0x001
- pwntools直接连接得到flag。
0x002 pwn_me_100years(1)
1 | from pwn import * |
0x003 pwn_me_100years(2)
1 | Arch: amd64-64-little |
考察格式化字符串漏洞以及PIE绕过方式。
通过这道题,学到挺多的。
对开启PIE保护的程序下断的方法
首先是对于开启PIE保护的文件,如果我们要使用gdb调试的话,需要这么下断点:
b *$rebase(相对基址偏移),这个相对基址偏移可以在IDA中看到,就是在IDA里面看到的指令地址。但是需要gdb运行程序以后才能下断,gdb里面r了以后程序会直接运行下去,一般来说程序都有提示输入的函数,这时候我们先r然后直接Ctrl + C,然后下断即可。或者通过
pie命令可以得到基址。

- 或者通过
vmmap或者libs命令得到基址,这俩命令是等价的。
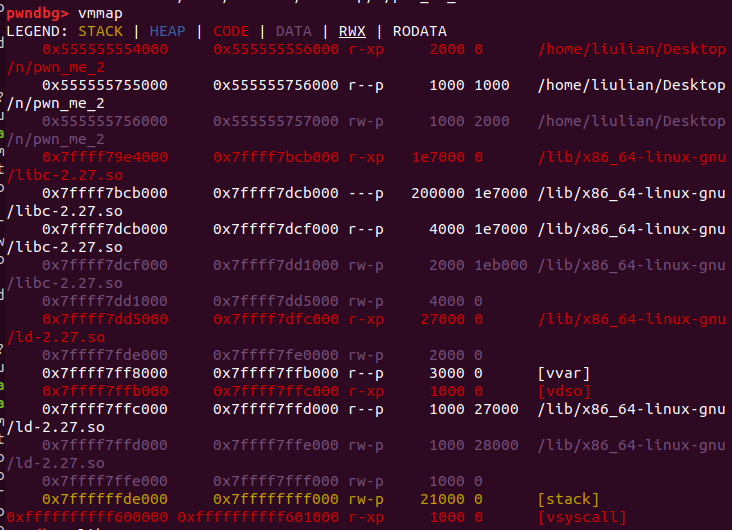
- 然后
真实地址 = 基址 + 偏移,通过常规下断方法即可对真实地址下断。
PIE绕过
通过动态调试,我们可以知道
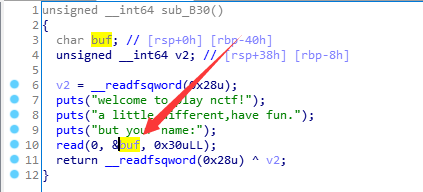 这里的
这里的buf与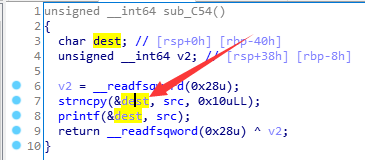 这里的
这里的dest是同一块区域。我们可以read读入0x30个字节,但由于strncpy函数会覆盖掉前16个字节,所以我们可以利用后0x30-16个字节。我们通过发送16个填充字符和一个
%p(用来泄露地址),得到这个地址,由于开启了PIE保护,所以这个地址每次重新加载程序的时候都会变的。所以我们需要计算出来这个地址跟基址的偏移(偏移保持不变),以不变应万变。
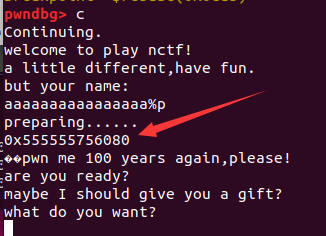
我们泄露出来的地址为
0x555555756080。由于我们的基址 =
0x555555554000。

所以偏移
offset = 0x202080。那么每次程序的基址就等于
我们每次泄露出来的地址减去偏移offset。
格式化字符串漏洞利用
剩下的就是格式化字符串漏洞了。
我们手动测出来格式化字符串漏洞的
offset = 6。下面构造payload,由于目标数值为0x66666666,太大了,我们分批来写。每次写入
0x6666即26214,占两个字节。所以我们的payload为:
1 | payload = '%26214c%10$hn%11$hn'#注意 %10$hn%11$hn,原因见下一行。 |
- 完整exp如下:
1 | from pwn import * |
0x03 Crypto
0x001 Keyboard
- 模拟手机九键输入法。
ooo yyy ii w uuu ee uuuu yyy uuuu y w uuu i i rr w i i rr rrr uuuu rrr uuuu t ii uuuu i w u rrr ee www ee yyy eee www w tt ee
- o对应9,o出现了三次,对应字母y,以此类推…
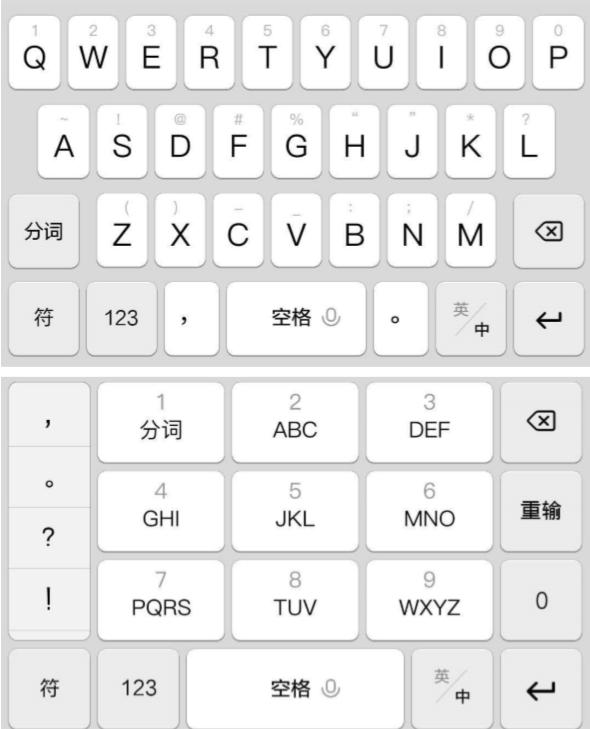

- 写个解密脚本得到flag。
1 | # -*- coding: UTF-8 -*- |
0x002 ChildRSA
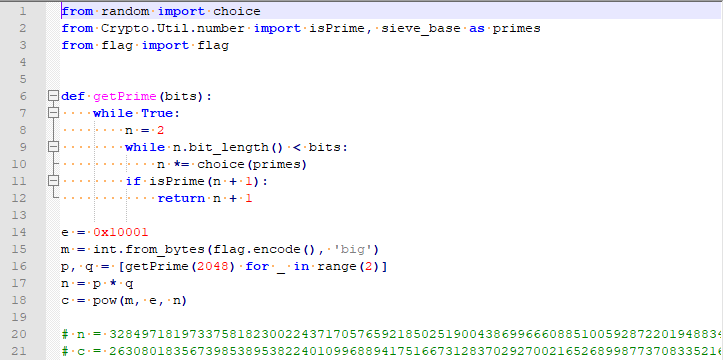
非预期解
根据题目,pq应该会比较相近。尝试yafu分解。
直接在命令行里面传入n的话,会提示
mismatched parens,我们新建一个n.txt,在里面写入n的值,注意最后要加换行!然后用在命令行用命令yafu-x64.exe "factor(@)" -batchfile n.txt。然后几秒钟后就得到了pq的值。

- 那么现在pqnec都知道了,直接求解m即可。
1 | import gmpy2 |
出题人的意思

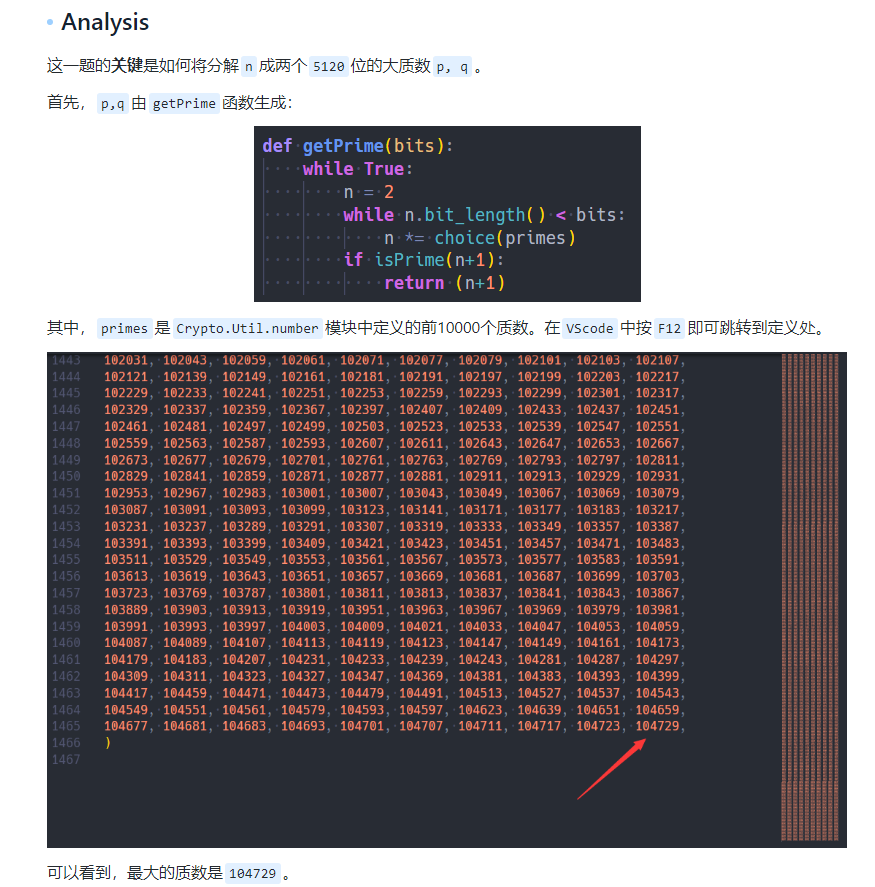


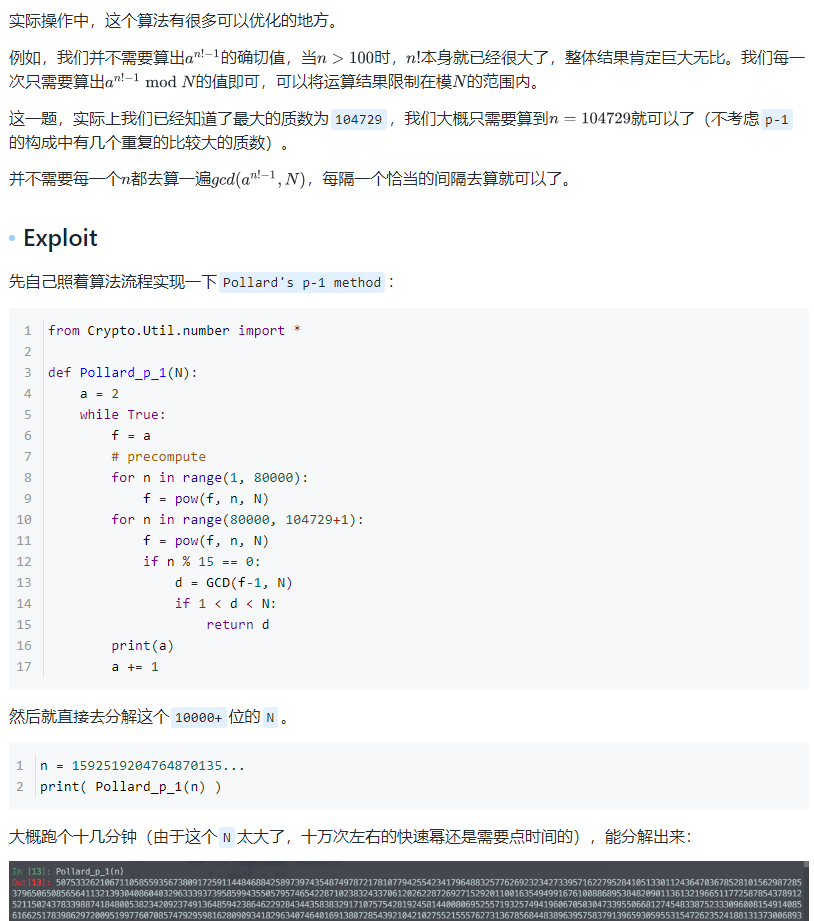
1 | from Crypto.Util.number import * |
- 然后就是正常的解密了。
0x003 BabyRSA
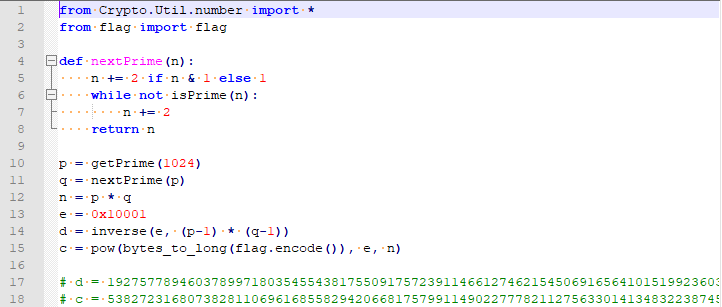
根据代码可以得知p和q是两个相邻的大素数。我们知道了d也知道e。
那么根据
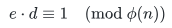 ,可以得到
,可以得到 ,即
,即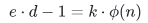 ,又因为
,又因为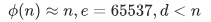 ,可得
,可得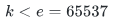 。
。那么就可以去爆破这个k,从而得到phi (n)。又因为pq是相邻两个大素数,大小差不多,那么
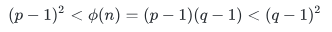 ,可以通过对phi (n)开根号,在根的附近寻找能够整除phi (n)的数,找到了就是p-1或者q-1,从而获得n,然后获得flag。
,可以通过对phi (n)开根号,在根的附近寻找能够整除phi (n)的数,找到了就是p-1或者q-1,从而获得n,然后获得flag。爆破k的脚本如下:
1 | # -*- coding: UTF-8 -*- |
注意,求根的时候不能用math.sqrt(),因为我们的数太大了,所以选用gmpy2.iroot来求根。
拿到n以后 我们知道了c、d、n,就能得到flag了。
1 | from Crypto.Util.number import * |
0x04 Misc
0x001 Pip install
- Win下
pip install nctf-2019-installme,会出现一个链接,打开链接下载.gz压缩包,在setup.py里面有flag的base64,解码即可。
0x002 a good idea
binwalk拿到to.png和to_do.png。
据说用Stegsolve的Image combiner可以拿到二维码。
脚本解题,脚本如下:
1 | # -*- coding: UTF-8 -*- |
- 拿到二维码扫码可得flag。
0x003 What’s this
- 从流量包里提取出来
What1s7his.txt,base64隐写解码得到flag。
0x004 键盘侠
- 解伪加密得到一个图片, binwalk一下拿到好多7z、zip,看了一下zip文件,实际上是个doc文件,拓展名改成doc以后里面内容如下:

base85解密得到flag。- python3的base64库里面自带b85decode, 但是python2里面没有。

