数学,如星空一般美丽又神秘

简介

RSA是1977年由Ron Rivest、Adi Shamir、Leonard Adleman一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。

RSA是目前最有影响力和最常用的公钥加密算法，它能够抵抗到目前为止已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。
RSA算法基于一个十分简单的数论事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开。
本文将介绍RSA算法所需的知识基础、RSA算法基本原理。

知识储备

RSA算法加解密其实就是两个公式，但是为了理解这两个公式我们需要学习数论中的四个概念：互质、欧拉函数、欧拉定理、模反元素，这四个概念都是非常好理解的，只需要有初高中的数学知识就能理解。

互质关系

互质整数是公约数只有1的两个整数,比如15和32,这说明不是质数也可以构成互质关系。
关于互质关系,有以下结论:

任意两个质数构成互质关系，比如13和61
一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10
如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57
p是大于1的奇数，则p和p-2构成互质关系，比如27和25
p是大于1的整数，则p和p-1构成互质关系，比如53和52
1和任意一个自然数是都是互质关系，比如1和99

欧拉函数

欧拉函数听起来很高大上，但其实非常简单，欧拉函数是小于x的整数中与x互质的数的个数，一般用φ(x)表示。例如φ(8)就等于4,因为8以内的与8互质的数只有1、3、5、7这四个数。
关于欧拉函数有几点性质:

特殊的，φ(1)=1。
如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。
如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则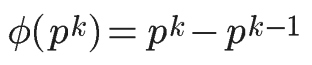比如 φ(8) = φ(2^3) =2^3 – 2^2 = 8 -4 = 4。
如果n可以分解成两个互质的整数之积,即n = p1 × p2,则φ(n) = φ(p1p2) = φ(p1) × φ(p2)。

欧拉定理

欧拉函数的用处，在于欧拉定理，而欧拉定理是RSA算法的核心。
欧拉定理指的是: 如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

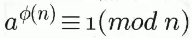
其中’≡’是恒等号(在这也可叫为同余号),表示该等式始终成立而与n、a的值无关。
这个式子的含义为:a的φ(n)次方除以n的余数为1。
欧拉定理的证明较为复杂,我们只需要记住这条结论就行,挺好记的。

模反元素

如果两个正整数a和n互质，那么一定可以找到整数b(不一定唯一)，使得 ab-1 被n整除，或者说ab除以n的余数是1。
即 ab≡1 (mod n), 这时，b就叫做a的“乘法逆元（乘法模反元素）”。
比如，5和17互质，那么7就是5的模反元素,同时24、41、58…都是5的模反元素，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

明文and密文

最后我们介绍一组概念。

明文(Plain Text):明文，是指没有加密的文字（或者字符串），属于密码学术语。
密文(Cipher Text):密文是加了密的的文字。

即明文是加密之前的文字。密文是对明文进行加密后的报文。

看得有点迷?没关系,后面有具体示例

RSA算法基本原理

RSA是一种非对称加密算法。非对称加密算法的优点我们会在后面的RSA加解密演示中介绍到。
在进行RSA加密与解密之前,我们先要有RSA密钥,即公钥和私钥。
我们用公钥对明文进行加密, 用私钥对密文进行解密。公钥是可以让所有人都知道的,但是私钥只能我们自己知道。

密钥生成规则

(1)随机选择两个不相等的质数p和q

我们选择61和53,在实际应用中,这两个质数越大就越难破解。

(2)计算p和q的乘积n

n = 61 * 53 = 3233
3233写成二进制是110010100001共12位,故该密钥是12位的,目前主流可选值：1024、2048、3072、4096…低于1024bit的密钥已经不建议使用（安全问题）。

(3)计算n的欧拉函数φ(n)

因为n = p*q,由欧拉函数的小性质 ,如果n = p × q且p、q互质,则φ(n) = φ(pq) = φ(p)φ(q)。
由于我们的p和q都是质数,再一次由欧拉函数的小性质如果n是质数，则 φ(n)=n-1,可得φ(p) = p-1 , φ(q) = q - 1。所以我们的φ(n) = (p-1)(q-1)
所以我们例子中的φ(n) = 60×52 = 3120。

(4)按照条件随机选择一个整数e

选择e的条件是 1< e < φ(n)，且e与φ(n) 互质。
本例中选取e = 17,但实际应用中e常常取65537 。

(5)计算e对于φ(n)的模反元素d

根据欧拉定理我们有:ed ≡ 1 ( mod φ(n) )
即 ed–kφ(n)=1
将e = 17,φ(n) = 3120代入可得:17d–3120k=1
这里我们采用拓展欧几里得算法求解d的值。

拓展欧几里得算法可用来求解线性同余方程a∗x≡c(modb) 且c=1的情况。我们可以把该方程转换成a∗x+b∗y=1这种形式。

此处给出求解代码:

# -*- coding: UTF-8 -*-
def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)
def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('modular inverse does not exist')
    else:
        return x % m

e = 17
phin = 3120
    
d = modinv(e,phin)
    
print 'd = ' + str(d)

这样求出我们的d = 2753。

(6) 将n和e封装成公钥,n和d封装成私钥

前面我们已经求出来了:

p = 61
q = 53; 或者写成p = 53,q = 61都可以。
n = pq = 3233
φ(n) = (p-1)(q-1) = 3120
e = 17; 满足1< e < φ(n)，且e与φ(n) 互质。
d = 2753;e对于φ(n)的模反元素d。

所以我们的公钥就是(n,e) = (3233,17),私钥就是(n,d) = (3233,2753)。

RSA算法可靠性分析

我们一共生成了六个数字：p、q、n、φ(n)、e、d，这六个数字之中，公钥用到了两个（n和e），其余四个数字都是不公开的。其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。
那么，有无可能在已知n和e的情况下，推导出d？

ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。
而φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。
而n=pq。只有将n因数分解，才能算出p和q。

综上,如果n可以被因数分解,那么就可以算出d,从而拿到私钥。
大数的因数分解是非常困难的。限制人类分解大整数的是计算机的计算能力，相信如果有一天真正的量子计算机问世后，又会引发一轮安全加密竞赛！

RSA加解密演示

情景导入

我们以经典的Alice和Bob的故事来导入情景。
Alice在学习了RSA算法以后,制作了公钥和私钥(假定和我们上面制作的公钥私钥一样),Alice将公钥发送给Bob并告诉Bob以后给自己发消息之前先用公钥进行加密，Alice自己保留私钥。

加密

假设某天Bob要给Alice发送一个字母’A’,Bob需要先将’A’转为ascii码65，所以m = 65。ps: m必须是整数(字符串可以取ascii值或unicode值)，且m必须小于n。
那么我们根据下图关系可得到密文c。

由于我们的公钥是(n,e) = (3233,17),那么有65^17≡c(mod 3233)(本文中的’^’均表示几次方而不表示异或),这样我们求得c = 2790,那么Bob就可以把c = 2790发送给Alice了。
这样即使有第三者截获了密文c,或者截获了公钥和密文c,由于第三者没有私钥,很难将密文c解密到明文m。此时非对称加密的优点便体现出来了。如果看得有点迷,没关系,咱们打个比方。
非对称加密就像Alice将一把已经打开的锁发送给了Bob而自己留着开锁钥匙,让Bob每次给自己发送消息的时候都用这把锁将消息锁住,当Alice收到消息后用只有自己才有的钥匙来解锁得到真正的信息。这样就算第三者劫持了密文和锁,因为没有钥匙,也很难很难拿到真正的消息。
假设我们用的对称加密,往往会把密钥和密文一同传给接收者,就像把钥匙和密文一起发送出去,这样如果一旦有第三者截获了密文和钥匙,就很容易利用密钥解密得到明文。

解密

当Alice拿到密文c = 2790,就可以用私钥根据下图关系可得消息m，也就是我们的明文。

接收者的私钥(n,d) = (3233,2753)，所以得到2790^2753 ≡ m(mod 3233)。从而可以解得m = 65,转换成字符就是我们的消息’A’。

再一例

如果我们的明文m不止一个字符,而是一段话(字符串),该如何发送呢？
假设Bob要给Alice发送"Hello",我们需要先str转hex得到0x48656c6c6f,转换为10进制则得到m = 310939249775。即 str->hex->十进制。
关于这里的str转hex,提供一个小方法,当然还有更简便的方法比如libnum.s2n: 我们可以遍历字符串中的每个字符,得到每个字符ascii码值的16进制,然后依次拼接,最后在拼接成的字符串前面加上0x,然后16进制转10进制。如果写成代码就是:

c = 'Hello'
res = '0x'
for i in c:
    res += hex(ord(i))[2:]
print 'm = ' + str(int(res,16))

由于我们前面也谈到了m必须小于n,但是显然我们这个例子里的m=310939249775大于n=3233,我们需要重新生成公钥和私钥。
生成过程略,这里直接列出我们的生成结果。

p = 999671
q = 999727
φ(n) = 999396090420
n = 999398089817
e = 65537
d = 529762121873

所以公钥为(n,e)=(999398089817,65537),私钥为(n,d)=(999398089817,529762121873)。
那么根据m^e ≡ c(mod n)即310939249775^65537 ≡ c(mod 999398089817),我们可以求得c = 274054322757。
那么Alice在拿到密文c = 274054322757以后,根据c^d ≡ m(mod n),即274054322757^529762121873 ≡ m (mod n)得到m = 310939249775。
那么我们就可以通过m转成我们的明文了。依然是提供几个方法,可能还有更好的方法~

print long_to_bytes(m)#需要引入库from Crypto.Util.number import *
print hex(m)[2:].replace(‘L’,’’).decode(‘hex’)